Incumbency Advantage
Historically, though not universally, incumbent politicians have an advantage over their challengers. The traditional explanation is that this is because the incumbent has name recognition, access to resources, the ability to take credit for public spending, etc. And this all makes sense, and might well be true. But it strikes me that you can actually generate a model of incumbency advantage with one simple supposition: good candidates win against bad ones. (Probably obvious but: "good" means good at being a politician, not good as a person).
For simplicity, let's say 1/2 of candidates nominated are bad and 1/2 are good. If a good candidate goes against a bad one, the good one wins; if both candidates are the same type (both bad, or both good), one of them wins at random.
Here are the odds of the different types of match-up in Year 0, where neither candidate is an incumbent:
| BLUE GOOD | BLUE BAD | |
|---|---|---|
| RED GOOD | 1/4 (Good wins) | 1/4 (Good wins) |
| RED BAD | 1/4 (Good wins) | 1/4 (Bad wins) |
For our purposes, it doesn't matter whether blue or red wins: the point is there is a 3/4 chance that the candidate who wins will be good, even though only 1/2 of candidates overall are good.
In the subsequent election, the incumbent will run again, while the challenger party will put up a new candidate with the usual odds of goodness. So, the challenger has a 1/2 chance of being good while the incumbent has a 3/4 chance of being good. This time, what we care about is the probability that the incumbent will win. The odds of each possible match-up are:
| INCUMBENT GOOD | INCUMBENT BAD | |
|---|---|---|
| CHALLENGER GOOD | 3/8 (Random winner) | 1/8 (Challenger wins) |
| CHALLENGER BAD | 3/8 (Incumbent wins) | 1/8 (Random winner) |
So the incumbent wins 3/8 times by being better, and an additional (3/8 + 1/8)/2 = 2/8 times by being equally-good or equally-bad as her opponent. Overall, the incumbent wins 5/8, or 62.5% of the time. We've derived an incumbency advantage just by positing that good candidates win against bad ones.
You might be wondering how sensitive this result is to the initial odds that a candidate will be good or bad. (You can insert your own joke here about the plausibility of an initial 1/2 chance candidate will be good). The answer – which was not preemptively obvious to me – is that the odds of incumbent winning in this model is a gentle curve going from 50% up to 62.5% and back again.
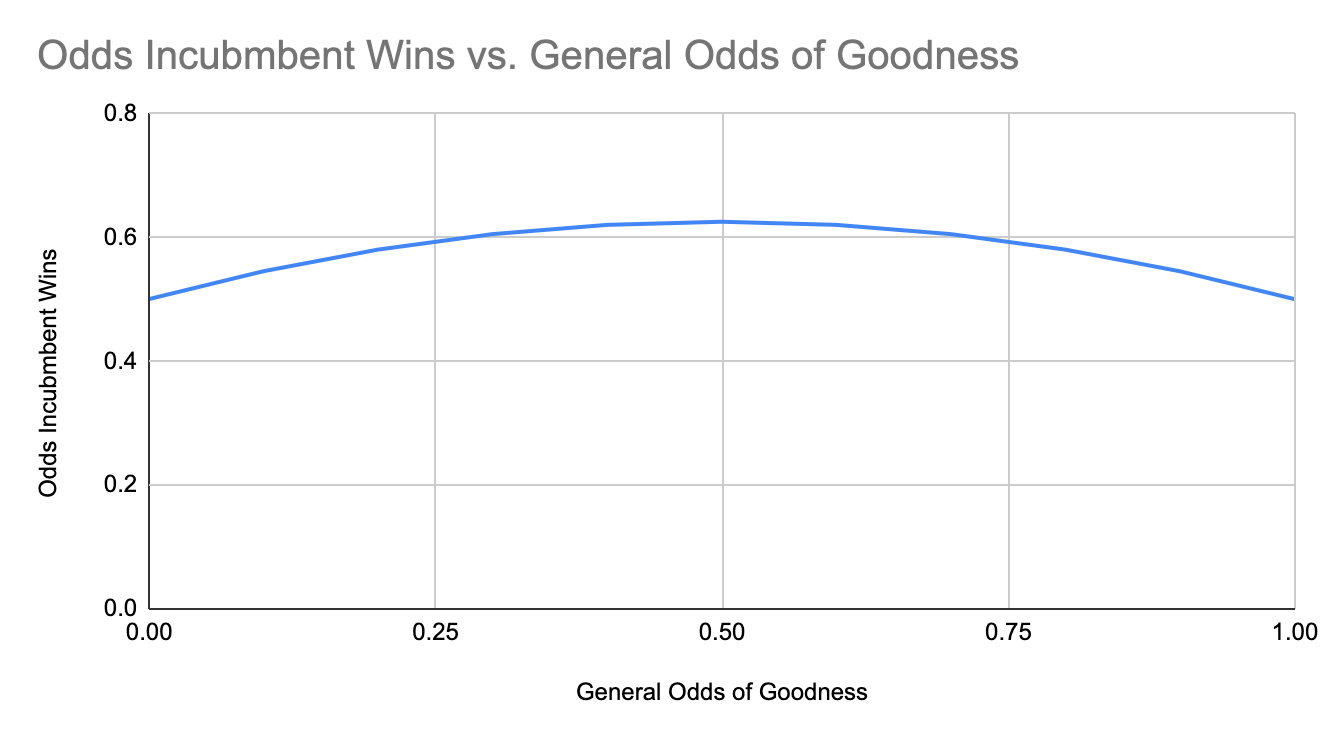
To me, the key insight is that incumbent politicians have survived a quasi-evolutionary process and proved themselves fitter than at least one opponent. This gives us some additional information that we don't have about the challenger, and which can create an incumbency advantage even absent any other factors. And, incidentally, this evidence becomes stronger if the role doesn't have term-limits, such that the next election is between either a multi-term incumbent or a challenger who beat a previous incumbent – with each election that features an incumbent, it becomes more and more likely that now-incumbent is a good politician. Which makes it more and more likely that, in the subsequent election, the now-incumbent will win.